Diffusion Model

Denoising Diffusion Probablistic Models

扩散模型已经成为了当下最火的生成模型，不仅在图像生成领域，许多其他模态的生成任务也开始广泛的应用扩散模型。而让该模型真正得到广泛应用的工作即为2020年所发表的论文《Denoising Diffusion Probablistic Models》

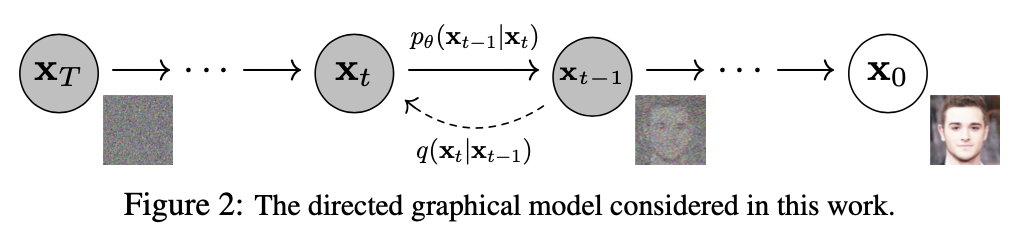
Reverse Process & Diffusion Process

如上图，Diffusion Model的核心便在于前向和逆向的两个过程。一般而言，Diffusion Models的形式为，联合分布即被称为reverese process。该过程在本工作中被定义为马尔可夫过程，从标准高斯分布开始，每一步均满足一个可学习的高斯分布，也即 而加噪过程则被固定为一个向原数据逐步添加高斯噪声的马尔可夫过程，即 其中为事先确定好的方差。如果令，，，那么很容易可以得到

那么，因此可以得到 到这里，我们有了任意时刻，给定时的分布，也就是所谓的diffusion process，显然我们更关心的则是reverse process，也就是分布，假设我们知道了该分布，那么从T时刻开始便可以一步一步去噪回原始的图像，这也是我们希望神经网络所学习到的东西，在推理过程中，即扮演了的角色，但遗憾的是，这个q分布实际上是不知道的，否则也不需要白费力气去训练一个神经网络出来，因此问题就转变为，该如何设计损失函数，使？

Loss Function

Diffusion采用最大似然的思想来进行优化，和VAE相同，由于难以直接求的期望，Diffusion也采取优化其变分下界的方法来进行最大似然，即 这里和VAE的部分相同，VAE中的即为这里的

我们有，而等式两边同时对做期望，因此有，注意到KL距离始终大于0，因此上式成立，令，则只需要最小化负的VLB即可

根据公式(1)和公式(2)，​，进一步的有 因此，实际上只需要约束和的KL散度即可，即为网络的输出，而只需要知道即可，那么 由扩散过程的马尔可夫性质，最终有 由公式(2)和(3)，则有 于是就得到了Diffusion Model理论上的损失函数

Simplification

我们关注公式(5)是否能够被进一步的简化。在Diffusion Model中，作者将前向过程的方差固定为超参数，因此前向的q分布是固定的，而在T足够大时为标准正态分布，因此是一个常数，在训练时可以被忽略

对于，作者直接把公式(1)中的固定为或，而只学习，由于两个高斯分布的KL散度可以写为，因此实际上只是优化之间的L2范数，将代入，损失函数的项都可以被写为 对应的，由于在训练过程中是已知的，我们可以把模型的输出改写为 因此损失项本质上就是在优化和之间的L2范式，这样我们的模型只需要预测噪声即可，也就是原论文中的Training和Sampling的伪代码：

L0

上面已经讨论过了和的情况，而则是如何满足给定时最大似然，也就是原图像的像素值，为此DDPM单独设置了一个从到的decoder来满足离散的最大似然。具体而言，假定图片像素已经被线性的映射到了[-1,1]之间，那么离散的似然概率可以写为 其中， 这样的话，最终就可以直接使用的结果作为无噪声的图片输出结果

参考

1. 变分推断
2. Diffusion Models：生成扩散模型
3. Diffusion Models：生成扩散模型-zhihu